Approximation polynômiale : le match !

De nombreux chapitres des programmes de mathématiques de l'enseignement supérieur sont consacrés aux problèmes d'approximation avec la question :

" comment approcher une fonction quelconque par une fonction simple comme un polynôme ?"

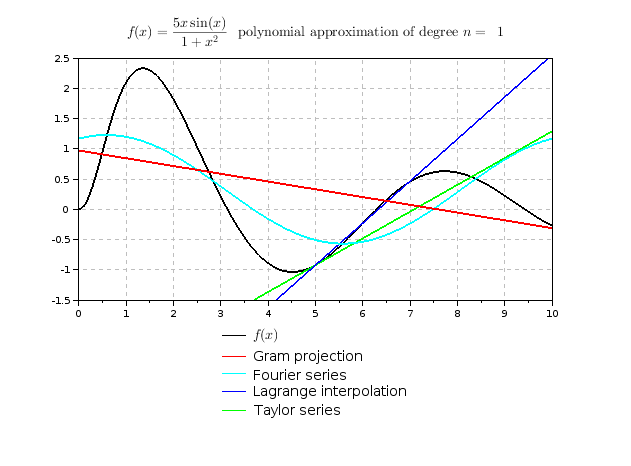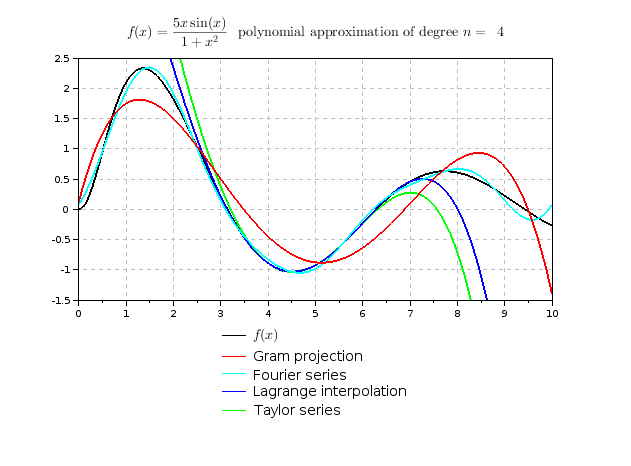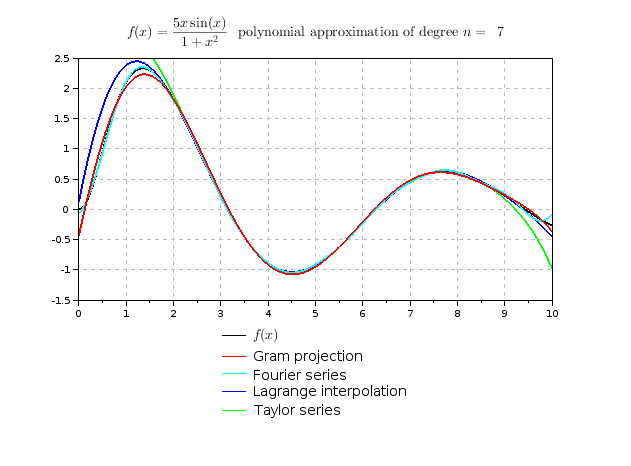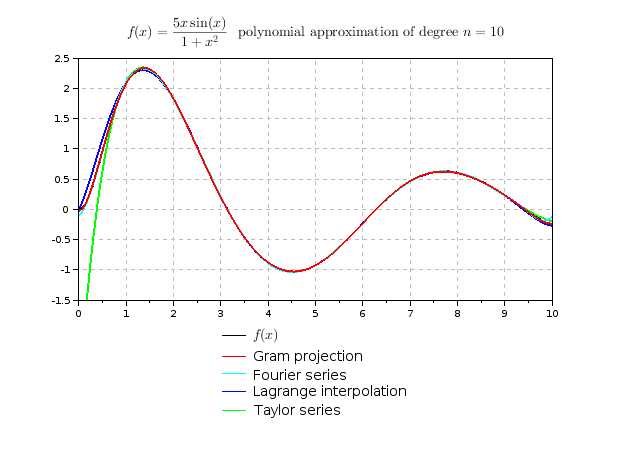
le cloisonnement des modules d'enseignement et l'hétérogénéité des formations précédemment suivies par les étudiants rend souvent difficile la comparaison entre ces différentes méthodes. C'est bien dommage car ce sujet est un bon exemple pour montrer comment un problème donné peut conduire à différentes méthodes  avec chacune leurs avantages et leurs inconvénients. Je me suis amusé à bâtir une petite comparaison de différentes méthodes pour la fonction $f(x)={5x\sin(x)\over 1+x^2}$  en utilisant le logiciel scilab:

Séries de Taylor
c'est souvent la première méthode enseignée, mais pas forcément la plus efficace, elle est vue dans les cours d'analyse et repose sur la formule de Taylor :

Théorème [formule de Taylor avec reste intégral] 
si $f\in C^{n+1}(I)$ avec $I=]x_0-\varepsilon,x_0+\varepsilon[,\varepsilon>0$ alors :
$$f(x)=\sum_{k=0}^n {f^{(k)}(x_0)\over n!}(x-x_0)^k+\underbrace{\int_{x_0}^x {f^{(n+1)}(t)\over n!}(x-t)^k dt}_{o\left((x-t)^n\right)}$$

approximation de taylor

On remarque que si rapidement l'approximation est très bonne  près de $x_0=5$, il n'en va pas de même sur les bord de l'intervalle [0,10]. En outre cette approximation nécessite de calculer les dérivées successives de f au point $x_0=5$. Ici comme on a une formule explicite pour $f$ on peut le faire en utilisant un logiciel de calcul formel comme maxima :

Le gros défaut de cette méthode  est que pour une fonction dont la formule est inconnue  il faudrait calculer des valeurs approchées de ces dérivées ce qui réduirait encore la précision ....

Interpolation de Lagrange

Une autre approche  consiste à chercher un polynôme passant par certains points de la courbe de f.  Trouver ce polynôme revient à résoudre un système d'équation linéaires   et le problème  peut être étudiée dans la plus part des cours d'algèbre linéaire de base.

Théorème [Matrice de Vandermonde]
Les coefficients $a_0,a_1,\dots,a_n$ seul polynôme $P(X)=a_0+a_1 X+\dots a_n X^n$ de degré n dont le graphe passe par les points $\{(x_i,y_i)\vert i=0,\dots, n\}$ s'obtient en résolvant le système d'équations :
$$\left\{
\begin{eqnarray*}
a_0+a_1 x_0+\dots+a_n x_0^n&=&y_0\\
a_0+a_1 x_1+\dots+a_n x_1^n&=&y_1\\
\vdots &\vdots&\vdots\\
a_0+a_1 x_n+\dots+a_n x_n^n&=&y_n\\
\end{eqnarray*}
\right.
\Rightarrow
\begin{pmatrix}
a_0\\ a_1\\ \vdots\\ a_n
\end{pmatrix}
=
\begin{pmatrix}
1&x_0&\dots&x_0^n\\
1&x_1&\dots& x_1^n\\
\vdots &\vdots &\vdots&\vdots\\
1&x_n&\dots& x_n^n\\
\end{pmatrix}^{-1}
\times
\begin{pmatrix}
y_0\\y_1\\\vdots\\y_n
\end{pmatrix}$$
la matrice de taille $n\times n$  du  système d'équations (matrice de Vandermonde) étant inversible si et seulement si les $x_i$ sont deux à deux différents.

On peut aussi voir ce problème  du point de vue des bases des espaces vectoriel :

Théorème [interpolation de Lagrange]  Soient $\{x_0,x_1,\dots,x_n\}\subset I$ alors la famille de Polynôme de degrés  $\{P_0,P_1,\dots,P_n\}\subset {\mathbb R}_n[X]$  définie par :
$$P_j(x)={\Pi_{i\neq j} (X-x_i)\over \Pi_{i\neq j} (x_j-x_i)}\Longleftrightarrow
P_j(x_i)=\left \{
\begin{array}{rcl}1 &si& x_i=x_j\\
0 & sinon&\\\end{array}\right.$$
est une base de l'espace vectoriel ${\mathbb R}_n[X]$   et le seul polynôme $P$ dont le graphe passe par les points $\{(x_i,y_i)\vert i=0,\dots, n\}$  est
$$P(X)=y_0 P_0(X)+\dots+y_n P_n(X)\Longleftrightarrow
P(x_i)=y_i,\forall i=0,\dots, n$$

Interpolation de Lagrange

Ici pas besoin de calculer de dérivées, seules les valeurs de f en différents points sont nécessaires, et il est possible d'approcher rapidement la fonction sur tout l'intervalle I=[0,10]. Il peut cependant apparaître des problèmes sur les bords de l'intervalle difficiles à éliminer, c'est le phénomène de Runge.

Projection Orthogonale et matrice de Gram

Pour améliorer la convergence des suites de polynôme il faut utiliser  une structure plus riche que la simple structure d'espace vectoriel  : un espace de Hilbert . Dans ce cadre on a une notion de distance et surtout d'orthogonalité qui permet de définir clairement la notion de "meilleur approximation" :

Théorème [Formule de Bessel]  Soit $H$ un espace de Hilbert muni de produit scalaire $\langle.,.\rangle$  et $B=\{e_i\vert i\in {\mathbb N}\}$  une base de $H$ (pas forcément orthogonale). On appelle :

•  $H_n={\rm Vect}(e_0,\dots,e_n)$ le sev engendré par les $n+1$ premiers vecteurs de $B$
• matrice de Gram $G$ la matrice de taille $(n+1)\times(n+1)$ définie par $G_{i,j}=\langle e_i, e_j\rangle$  

alors pour tout $f\in H$ la projection orthogonale  de $f$ sur $H_n$,   définie comme la fonction $g\in H_n$ la plus proche de $f$ (aus du produit scalaire de $H$) :
$$\Vert f-g\Vert_H={\rm min}_{h\in H_n}\Vert f_h\Vert_H$$
est $ g=\sum_{k=0}^n g_k e_k $ dont les coordonnées dans la base $B$ sont solutions du système :
$$\begin{pmatrix}
\langle f, e_0\rangle\\ \langle f, e_1\rangle \\\vdots\\ \langle f, e_n\rangle
\end{pmatrix}
=G\times
\begin{pmatrix}
g_0\\g_1\\\vdots\\g_n
\end{pmatrix}
\Rightarrow
\begin{pmatrix}
g_0\\g_1\\\vdots\\g_n
\end{pmatrix}
=G^{-1}\times
\begin{pmatrix}
\langle f, e_0\rangle\\ \langle f, e_1\rangle \\\vdots\\ \langle f, e_n\rangle
\end{pmatrix}
$$

Dans le cas ou la base est orthonormée  la matrice $G$ est la matrice identité et la fonction $g$ s'exprime tout simplement par la formule de Bessel $ g=\sum_{k=0}^n \langle f,e_k\rangle e_k$. Mais il est tout aussi simple d'inverser la matrice $G$ que de calculer une base orthonormée  pour le produit scalaire.

Projection orthogonale 

Dans cet exemple j'ai pris $H={\mathbb L}^2([0,10])$ avec le produit scalaire usuel :
$$\langle f,g\rangle =\int_0^{10} f(x) \overline{g(x)} dx $$
et la base canonique constituée des monômes  $B=\{1;X;X^2;\dots \}$. La méthode  semble peu précise pour $n$ petit mais donne rapidement un résultat très précis sur toute la longueur de l'intervalle!


Séries de Fourier

Les séries de Fourier sont un cas particulier de projection orthogonale sur un sous espace vectoriel de ${\mathbb L}^2([0,10])$ généré par les fonctions $x\mapsto \exp(2i\pi kx/T)$ avec $k=-n,\dots,0\dots,n$  (qu'on appelle polynômes trigonométriques).  La convergence de la série de Fourier vers la fonction $f$   pour la norme hilbertienne repose là encore sur la projection au sens du produit scalaire usuel de ${\mathbb L}^2([0,10])$. Mais comme la base utilisée est orthogonale la formule s'exprime simplement par la l'égalité de Parseval mais on a aussi la convergence ponctuelle d'après le théorème de Dirichlet (voir mon billet Jouons avec les séries de Fourier!)

convergence des séries de Fourier

La convergence est assez rapide sauf aux points $x=0$ et $10$  car ici  lorsqu'on périodise la fonction $f$ en répétant son graphe sur l'intervalle [0,10]  comme motif principal, le raccordement  aux points $x=k\times 10,k\in{\mathbb Z}$ n'est pas continue car $f(0)\neq f(10)$ la série de Fourier converge donc vers $f(0)+f(10)\over 2$ d'après le théorème de Dirichlet.