Calculer les valeurs/vecteurs propres d'une matrice est un des problèmes les plus importants en mathématiques, il possède des applications dans de nombreux problème de physique aussi bien qu'en informatique (comme le calcul du PageRank !). La méthode classique du calcul exact des valeurs/vecteurs propres utilisant le calcul du polynôme caractéristique est en pratique inutilisable dès que la taille des matrices augmente, dans ce cas on doit se tourner vers des méthodes itérative qui ne calculent qu'une approximation des valeurs/vecteurs propres. Parmi ces méthodes l'une des plus efficaces est la méthode QR . Son implémentation est très simple, à tel point que son fonctionnement peut paraître relever de la magie ! C'est typiquement le genre de résultat mathématique où une visualisation "dynamique" de l'algorithme peut permettre de mieux en comprendre les mécanismes.
| Méthode QR appliquée à une matrice 10x10 |
$\epsilon=$ seuil de précision
A_0=A (matrice réelle de taille nxn)
$\tilde{Q}_0=Id_n$
tant que $\max_{i>j}|(A_n)_{i,j}|>\epsilon $
calculer la décomposition QR de $A_n$ : $A_{n}=Q_nR_n$
puis calculer $A_{n+1}=R_nQ_n$
$\tilde{Q}_{n+1}=Q_n\tilde{Q}_n$
Pour obtenir l'animation on affiche à chaque étape la matrice $A_n$ comme si c'était une image :A_0=A (matrice réelle de taille nxn)
$\tilde{Q}_0=Id_n$
tant que $\max_{i>j}|(A_n)_{i,j}|>\epsilon $
calculer la décomposition QR de $A_n$ : $A_{n}=Q_nR_n$
puis calculer $A_{n+1}=R_nQ_n$
$\tilde{Q}_{n+1}=Q_n\tilde{Q}_n$
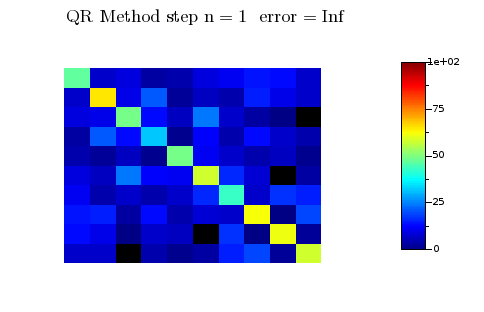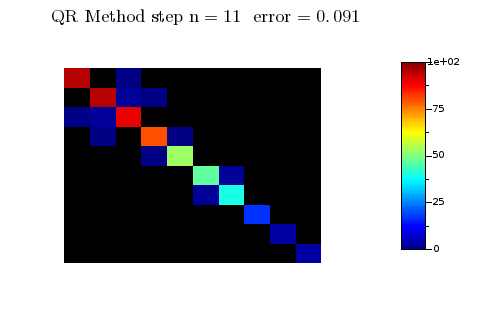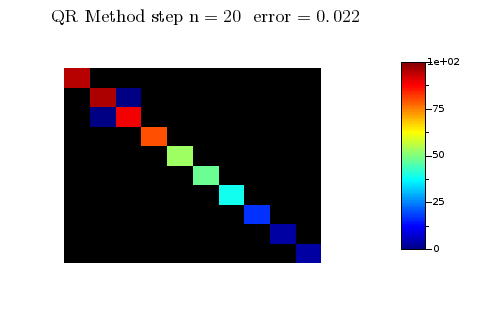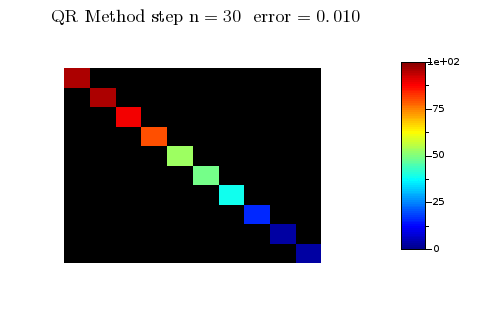
- chaque case (i,j) de la matrice A correspond à un pixel de l'image en position i-ième ligne j-ième colonne
- le pixel (i,j) est colorié avec une palette de couleurs en fonction de la valeur de $\vert A_{i,j}\vert $ donnée par l'échelle à droite (de 0 pour le noir-bleu à plus de 100 pour le rouge-blanc)
On voit bien sur l'animation que tous les coefficients de la matrice $A_n$ qui sont "sous" la diagonale tendent vers 0 assez rapidement : c'est la clé du fonctionnement de cet algorithme. La démonstration de ce résultat est en général très compliquée et il faut au préalable rappeler ce qu'est la décomposition QR d'une matrice :
théorème (décomposition QR)
Soit $A$ une matrice à coefficients réels alors on peut décomposer $A=QR$ avec :
Soit $A$ une matrice à coefficients réels alors on peut décomposer $A=QR$ avec :
- $Q$ une matrice orthogonale $~^tQQ=Id$
- $R$ une matrice triangulaire supérieure
La décomposition QR d'une matrice peut s'obtenir par la méthode de Householder , ou plus simplement en appliquant le procédé de Gram-Schmidt aux vecteurs colonnes de $A$ (pour le produit scalaire usuel de ${\mathbb R}^n$). À partir de là il est assez facile de montrer que :
- les matrices $A_n$ sont semblable à la matrice $A$
$$A_{n+1}=R_nQ_n=~^tQ_nA_nQ_n=\dots= ~^t\tilde{Q}_{n}AQ\tilde{Q}_n$$
c'est pour cette raison que les différentes matrices ont le même spectre et si elles tendent vers une matrice triangulaire supérieurs les valeurs propres sont les valeurs sur la diagonale. - par récurrence on montre aussi la relation :
$$A^n=(Q_1\dots Q_n)(R_n\dots R_1)=\tilde{Q}_n(R_n\dots R_1)$$
c'est à partir de cette formule qu'on peut montrer que la méthode QR utilise les mêmes principe que l'algorithme de la puissance itérée, pour calculer des approximations de chaque valeur/vecteur propre.
$$\vert \lambda_1 \vert\geq \vert \lambda_2 \vert\geq \dots \vert \lambda_p \vert
~~~~ a= \min_{i=1,\dots,p-1}\left\vert{\lambda_{i+1}\over\lambda_i}\right\vert$$
alors l'erreur commise sur les vecteurs/valeurs propres à la n-ième étape est en $O\left(a^n\right)$. La méthode QR marchera donc d'autant mieux que les valeurs propres sont "bien séparées". Cette estimation permet aussi de comprendre les cas d'échecs de la méthode QR :
- s'il y a une valeur propre multiple on a alors $\left\vert{\lambda_{i+1}\over\lambda_i}\right\vert=1$ donc $a^n\not\to 0$ et la convergence de la méthode n'est pas assurée
- s'il y a une valeur propre nulle $\left\vert{\lambda_{i+1}\over\lambda_i}\right\vert$ n'est même pas défini, et la décomposition QR dans ce cas est un peu ambiguë .
- s'il y a des valeurs propres complexes, elles sont nécessairement conjuguées deux à deux et pour ces deux valeurs propres on a $\left\vert{\lambda_{i+1}\over\lambda_i}\right\vert=1$ ce qui pose le même problème que pour une valeur propre multiple
Il y a un cas particulier où la méthode QR va converger: celui des matrices symétriques, en effet dans ce cas on sait que la matrice est diagonalisable (même si elle a des valeurs propres multiples)
théorème spectral Soit $A$ une matrice carrée nxn à coefficients réels et symétrique $~^tA=A$ alors
- toutes les valeurs propres de $A$ sont réelles
- on peut construire une base orthonormée de vecteurs propres de $A$
Dans ce cas il n'y a donc pas d'obstacle à la convergence de la méthode QR et on a même que
- la suite de matrices $A_n$ converge vers une matrice diagonale composée des valeurs propres de $A$
- la suite $\tilde{Q}_n$ converge vers une matrice orthogonale correspondant aux vecteurs propres de $A$
On peut aussi remarquer que l'algorithme QR trie les valeurs propres sur la diagonale dans l'ordre décroissant .

Aucun commentaire:
Enregistrer un commentaire
Pour écrire des formules mathématiques vous pouvez utiliser la syntaxe latex en mettant vos formules entre des "dollars" $ \$....\$ $ par exemple :
- $\sum_{n=1}^\infty {1\over n^2}={\pi^2\over 6}$ s'obtient avec \sum_{n=1}^\infty {1\over n^2}={\pi^2\over 6}
- $\mathbb R$ s'obtient avec {\mathbb R} et $\mathcal D$ s'obtient avec {\mathcal D}
- pour les crochets $\langle .,. \rangle$ dans les commentaires utilisez \langle .,. \rangle
vous pouvez écrire du html dans les commentaires :
- italique <i> ... </i> gras <b> ... </b>
- lien <a href="http://adresse "> .... </a>