Depuis quelques temps je suis un compte Twitter appelé improov_Maths qui diffuse des questions mathématiques de type concours CPGE à la formulation très courte et de difficultés variées. Je me suis pris au jeux de résoudre ces questions, surtout quand elles proposent des calculs de séries comme celle ci-dessous, et bien sûr le tout en moins de 288 caractères!
Le niveau des questions proposées est matérialisé par un code couleur vert-bleu-rouge-noir du plus
simple au plus difficile. Les deux derniers niveaux
sont souvent très difficiles si vous ne connaissez pas parfaitement le domaine
correspondant des maths. La question ici n'est donc pas si simple à résoudre mais ça parle de séries et comme j'ai écrit beaucoup de billets sur le calcul des séries, sans jamais avoir rencontré cette série, c'est donc un défi pour moi!
\[\sum_{n\geq 1} {n^{n-1}e^{-n}\over n!}\]
Avant toute chose je commence par m'assurer que la série converge (ça sera utile plus loin). Comme la série est positive le plus simple est de chercher un équivalent à l'infini ce qui est facile ici si on connaît la formule de Stirling pour évaluer le $n!$:
\[ {n^{n-1}e^{-n}\over n!}
\sim_\infty {n^{n-1}e^{-n}\over \left({n\over e}\right)^n\sqrt{2\pi n}}
= {1\over n\sqrt{2\pi n}}={\mathcal O}\left({1\over n^{3/2}}\right)\]
\sim_\infty {n^{n-1}e^{-n}\over \left({n\over e}\right)^n\sqrt{2\pi n}}
= {1\over n\sqrt{2\pi n}}={\mathcal O}\left({1\over n^{3/2}}\right)\]
le critère de Riemann suffit donc à justifier la convergence de la série ... mais ne permet pas de la calculer évidement. Pour la calculer une série à termes positifs il n'y a que 2 pistes :
- identifier la série à une série télescopique
\[ \sum_{n\geq 1}{n^{n-1}e^{-n}\over n!}=\sum_{n\geq 1}u_{n+1}-u_n=-u_1\] - identifier la série à une série entière (pour un $x$ bien choisi)
\[\sum_{n\geq 1} {n^{n-1}e^{-n}\over n!}=\sum_{n\geq 1} a_n x^n\]
\[W(x)= \sum_{n\geq 1} {(-n)^{n-1}\over n!} x^{n}\]
je n'ai pas de suite reconnu ce développement en série entière, j'ai d'abord essayé de me ramener à exprimer le terme $ {n^{n-1}\over n!}$ sous forme d'un calcul d'intégrale (car il ressemble beaucoup à celui qu'on calcule dans le problème dit du "Sophomore's Dream" ) mais rapidement j'ai retrouvé qu'il s'agit du développement en série entière de la fonction W de Lambert qui est définie de manière implicite par :
\[W(x)=z\Leftrightarrow x=z e^z=W^{-1}(z)\]
le rayon de convergence de cette série entière se trouve facilement par le critère de D'Alembert :
\[{1\over R}=\lim_{n\to\infty}\left\vert {a_{n+1}\over a_n}\right\vert
=\lim_{n\to\infty} {(n+1)^{n}\over (n+1)!}\times {n!\over n^{n-1}}
=\lim_{n\to\infty} \left(1+ {1\over n}\right)^{n-1}=e
\Rightarrow R={1\over e}\]
On va donc obtenir que :
\[ \sum_{n\geq 1} {n^{n-1}e^{-n}\over n!}
= -\sum_{n\geq 1} {n^{n-1}\over n!} \left(-{1\over e}\right)^{n}
= -W\left(-{1\over e}\right)=1\]
car
\[-1\times e^{-1} =W^{-1}(-1)\Leftrightarrow -1=W\left(-{1\over e}\right)\]
La convergence de la série a été vérifiée au départ, on peut donc utiliser le théorème de convergence radiale d'Abel pour justifier que la valeur de la série entière est bien W(-1/e) ce qui n'est pas automatique quand on se place en un $x$ sur le bord du disque de convergence
Si vous aimez ce genre de questions n'hésitez pas à visiter le site web mathopera qui regroupe toute la banque de questions diffusée par le compte twitter improov_Maths


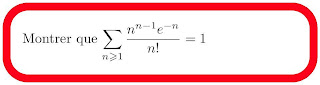
Merci !!!!! Très intéressant !!!!
RépondreSupprimerJe me suis déjà inscrit dans le compte de improov_Math !!!!!!
Je ne le connaissais pas !!!!!!!!