profilage de fonction avec scilab

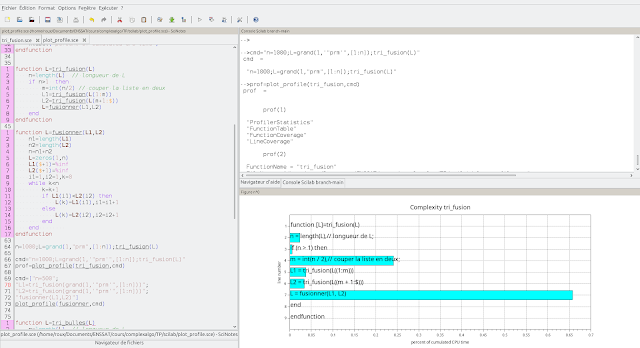
Quand on s'intéresse à la complexité des algorithmes il est intéressant de pouvoir confronter la théorie avec la pratique en vérifiant  quel est le temps d'exécution réel d'un programme et comment ce temps est réparti entre les différentes opérations. Il existe des outils de profilage de code qui permettent d'analyser le coût de chaque ligne de code dans un programme (coût du temps de calcul du processeur ou en mémoire).  Scilab possède quelques fonctionnalités dédiées à ce sujet, que j'avais documenté il y a plus de 10 ans , mais qui ont été complètement remanié. Le développement de Scilab semblant retrouver de l'activité, je me suis donc intéressé aux capacités des nouvelles fonctions de profilage et à l'exploitation graphique des résultats.

 

marpit pour remplacer powerpoint ou beamer

Utiliser un support projeté lors d'un exposé ou d'une réunion est devenu quelque-chose d'implicite. Dans ce domaine PowerPoint ™® ©  bénéficie d'une position hégémonique alors que c'est un outil propriétaire, lourd à utiliser et au  comportement parfois aléatoire (d'expérience "j'ai un problème avec le powerpoint" est la phrase la plus utilisée en exposée). Même si je travaille dans un écosystème ou LaTeX est l'outil le plus puissant pour la création de mes supports, qui m'amène donc à utiliser Beamer, j'ai souvent besoin de quelque-chose de plus léger et rapide. C'est comme ça que j'ai découvert Marp il y a quelques années. Au départ il s'agissait d'un éditeur Markdown spécialement adapté pour la réalisation de slides, mais le projet s'est mué en un préprocesseur marpit (comme pandoc) très efficace mais peut-être moins facile à prendre en main.

Queue de poussière vs Queue de plasma

L'actualité cométaire  a été bien chargée ces dernières semaines avec la comète C/2023A3 Tsuchinshan-ATLAS, l'occasion de faire de belles images mais aussi d'expliquer les phénomènes physiques complexes qui régissent l'apparence des comètes. Une des questions qui revient souvent est : pourquoi les comètes ont souvent deux queues ? De quoi sont-elles constituées ? Pourquoi  ont-elle des couleurs différentes ? Pourquoi pointent-elles dans des directions différentes ? Des questions auxquelles ont peut répondre par une simple étude de l'ordre de grandeur des forces en présence !

Comète C/2023A3 Tshushinchan-ATLAS le 22/10/2024

Divergences entre matlab et octave

Matlab™ ©®  est un des premiers logiciel de calcul numérique créé à la fin des années 80, il reste très utilisé dans le domaine industriel  malgré une syntaxe parfois archaïque et l'existence d'alternatives libres comme GNUoctave, Scilab, ou même Python! Chaque année quand je dois utiliser ce logiciel pour illustrer des cours de calcul numérique, je prépare mes scripts avec GNUoctave et évidement lors des TP je découvre de nouvelles  aberrations "fonctionnalités" toujours plus stupéfiantes  ...

comportement différent entre matlab et GNUoctave
lors de la résolution d'un système linéaire 

Occultation de Saturne par la Lune au smartphone!

Tôt le matin du 21 Août 2024  la Lune a occulté la planète Saturne, un phénomène relativement courant mais que je n'avais pas pu observer jusqu'ici ni prendre en photo. Un vide enfin comblé et l'occasion de voir que le smartphone  peut servir de capteur pour l'astronomie pour ce type de prise de vues très particulières.

6h27 Saturne réapparaît après occultation par la lune le 21/08/24

Aurores Boréales du 10-11 Mai 2024

 J'avais eu la chance d'observer des aurores boréales depuis la Bretagne en 2001 et 2003 près de 20 ans plus tard j'ai eu droit d'en observer de nouveau, dans la nuit du 10-11 Mai 2024, qui ont été massivement relayées dans les médias. L'occasion de vous faire un petit article sur le sujet et de vous donner les bons conseils pour en observer vous aussi.

petit film de l'aurore boréale du 10-11 mai 2024

Fonction hyperfactorielle et constante de Glaisher-Kinkelin

La formule de Stirling est le premier exemple de formule asymptotique qu’on rencontre en mathématiques. Il en existe d’autres tout aussi impressionnantes comme la formule de Moser-Wyman pour les nombres de Bell ou la formule asymptotique pour l’hyperfactorielle . Cette fonction hyperfactorielle est définie sur $\mathbb{N}^*$ de manière très analogue à la factorielle et possède un équivalent explicite analogue à la formule de Stirling $$H(n)=\prod_{k=1}^n k^k\sim_\infty A\left({n\over \sqrt{e}}\right)^{n^2\over 2} n^{{n\over 2}+{1\over 12}}$$ la constante $A$, dite constante de Glaisher-Kinkelin, admet une forme close assez compliquée faisant intervenir $e,\pi,\gamma$ et la fonction $\zeta$ dont on connaît 500000 décimales $A=1,28242712910062263687\dots$. C’est un bon exercice de calcul asymptotique que de démontrer ce résultat et d’encadrer la constante de Glaisher-Kinkelin avec pour principal outil la formule d’Euler-Maclaurin.

 

Les pionnières du calcul numérique et de l'informatique

Comme tout les ans le 8 Mars, décrété journée internationale des droits des femmes par l'ONU, est l'occasion de dénoncer le manque de féminisation des secteurs liés aux sciences, au numériques et à l’ingénierie. La situation qui n'était déjà pas très bonne en France, elle s'est encore dégradée avec la réforme du BAC et la situation inquiète même maintenant les organisations patronales dans l'industrie, c'est dire ! Dans l'enseignement supérieur chacun essaie d'apporter ça contribution pour combattre le préjugés sexistes  qui perdure dans les sciences, à moi d'apporter la mienne (toute modeste). A force de dénoncer l'absence des femmes en mathématiques et dans le numérique on finit par oublier qu'elles n'en ont jamais été absentes mais que bien souvent leur travail a été invisibilisé. Rien de mieux que de faire de jolis posters pour rappeler cela!

 

                




















alors connaissez vous  ces femmes ?

Fonction Dilogarithme et problème de bâle

J’ai toujours été fasciné par la formule $\sum_{k>0}{1\over k^2}={\pi^2\over 6}$, il existe beaucoup de preuve : un grand nombre utilisent les séries de Fourier, d’autre des relations entre coefficient et racines de polynômes, …, j’y ai consacré quelques billets dont une preuve n’utilisant qu’une série télescopique et une majoration d’intégrale ici ! Inversement on peut démontrer de manière très directe cette formule en utilisant toute la puissance de l’analyse complexe, c’est l’occasion de parler de la fonction holomorphe sous-cotée : la fonction Dilogarithme.

mes 500 premiers km de vélotaf

Les déplacements à vélo en ville prennent de plus en plus d'importance, mais ce modèle est-il possible en campagne ?  Beaucoup d'avis divergent sur le sujet à un moment où les déplacements doux, sans voiture, sont de plus en plus à la mode. Une seule manière de se forger un avis pertinent : Essayer !